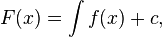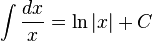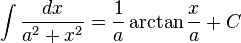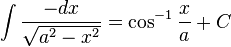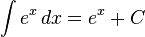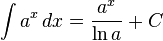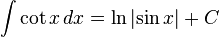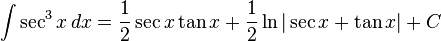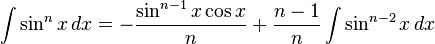Matematik Dünyası: 2011

16 Mayıs 2011 Pazartesi

integral aslında birçok işe yarar ama artık günümüz çağı öyle bir düzeydedirki teknloji makinaları bize bütün işlemleri yapılmış şekilde ürünü sunar..fakat gerçekten integralin kapsamı oldukça geniştir..adında anlaşılacağı gibi integre etmektir.sen noktaları integre ettiğinde doğruyu, doğruyu integre ettiğinde düzlemi, düzlemi integre ettiğinde de hacmi bulursun..ya da başka bir deyişle bunların integrasyon değişkenine göre fonksiyonlarını bulursun..

yani bütün anlattıklarım ne anlama geliyor..lise boyunca daire çember dışında hep doğru düz ve pürüzsüz şekilleri incelediğimiz için integral ve bu gibi hesaplar aklımızın ucundan bile geçmedi.ama gelgelelim hiçbir geometrik şekile benzemeyen tamamen keyfi kesitelere sahip demir bir nesnenin hacmini öle kolay kolay küpün hacmini bulur gibi bulamazsınız. bunun için nesnedeki en küçük noktanın hacminden başlayıp (noktanın hacmi derken en küçük hacmi taşıyan parçacığın) bu noktaları toplayıp (integre edip) cismin hacmine ulaşıcaksınız...

arkadaş çok haklısın.

ne işe yaradığı belli değil diyen arkadaşlara da bir iki örnekle anlatayım.
mesela işten eve geldin çekyata uzanıp, ayaklarını dinlendirecen, hele dur bakalım...

çekyatın oynar aksamındaki gerilmelerin; o aksamdaki dağılımı hesaplanmasa, binen kuvvetin ne tür burulmalara, çeki veya basılara sebep olacağı önceden hesaplanmasa; ekonomik olsun diye rastgele bir aksam kullanılsa, o çekyatda bir kere uzanabilirsiniz.
bindiğiniz araçlar, dinlediğiniz radya dinletisi, yayın araçları, alıcılar hep integral bilgisi sayesinde hayat bulmuştur.
bir geminin yüzey formu, ağırlığı, hacmi, stabilitesi, dış etkilere olan mukavemeti ve bunun gibi bir çok kuvvetler altındaki farklı tepkileri, integral sayesinde hesaplanır.

bu hesaplamalarda İntegral sadece bir araçtır. amaç değil. integral kullanım mantığı, kullanıcının belirlenmiş hedeflerine ulaşmak için kullanacağı bir doğrulama aracıdır.
bu sebeple, üniversitelerimizde gösterilen integral tabanlı ders içeriklerinde, öğrencilerin alan bilgisi dahilinde, integralle ilgili hangi yaklaşımları kullanması gerektiği öğretilirse; mühendislik veya diğer alan formasyonları daha iyi kazandırılmış olacaktır.

aklıma gelen (biraz sıkıldınız galiba, son kez...) bir taş ocağı, koca dağ...
ortalama yoğunluğu belli diyelim sıfır hattına kadar ki, kullanılabilir miktar hesaplanacak, işte integral; burada işinize yarayacak.
artık simson metodu kullanır mısınız, gaus metodu mu yardımcı olur

, yoksa başka yardımcı alan bilgileri mi, o size kalmış.
bundan sonra saate bakarken, veya televizyon izlerken, olmadı çatal kullanırken; integrale teşekkür etmeyi unutmayalım.

Günlük yasamda integral

Aklıma gelen bir taş ocağı, koca dağ...
ortalama yoğunluğu belli diyelim sıfır hattına kadar ki, kullanılabilir miktar hesaplanacak, işte integral; burada işinize yarayacak.
artık simson metodu kullanır mısınız, gaus metodu mu yardımcı olur, yoksa başka yardımcı alan bilgileri mi, o size kalmış.
bundan sonra saate bakarken, veya televizyon izlerken, olmadı çatal kullanırken; integrale teşekkür etmeyi unutmayalım.

resımlerle integral

GÜNLÜK YASAMDA İNTEGRAL

İntegral Günlük Hayatta Nerelerde Kullanılır?
integral aslında birçok işe yarar ama artık günümüz çağı öyle bir düzeydedirki teknloji makinaları bize bütün işlemleri yapılmış şekilde ürünü sunar..fakat gerçekten integralin kapsamı oldukça geniştir..adında anlaşılacağı gibi integre etmektir.sen noktaları integre ettiğinde doğruyu, doğruyu integre ettiğinde düzlemi, düzlemi integre ettiğinde de hacmi bulursun..ya da başka bir deyişle bunların integrasyon değişkenine göre fonksiyonlarını bulursun..

yani bütün anlattıklarım ne anlama geliyor..lise boyunca daire çember dışında hep doğru düz ve pürüzsüz şekilleri incelediğimiz için integral ve bu gibi hesaplar aklımızın ucundan bile geçmedi.ama gelgelelim hiçbir geometrik şekile benzemeyen tamamen keyfi kesitelere sahip demir bir nesnenin hacmini öle kolay kolay küpün hacmini bulur gibi bulamazsınız. bunun için nesnedeki en küçük noktanın hacminden başlayıp (noktanın hacmi derken en küçük hacmi taşıyan parçacığın) bu noktaları toplayıp (integre edip) cismin hacmine ulaşıcaksınız...

ne işe yaradığı belli değil diyen arkadaşlara da bir iki örnekle anlatayım.
mesela işten eve geldin çekyata uzanıp, ayaklarını dinlendirecen, hele dur bakalım...
çekyatın oynar aksamındaki gerilmelerin; o aksamdaki dağılımı hesaplanmasa, binen kuvvetin ne tür burulmalara, çeki veya basılara sebep olacağı önceden hesaplanmasa; ekonomik olsun diye rastgele bir aksam kullanılsa, o çekyatda bir kere uzanabilirsiniz.
bindiğiniz araçlar, dinlediğiniz radya dinletisi, yayın araçları, alıcılar hep integral bilgisi sayesinde hayat bulmuştur.
bir geminin yüzey formu, ağırlığı, hacmi, stabilitesi, dış etkilere olan mukavemeti ve bunun gibi bir çok kuvvetler altındaki farklı tepkileri, integral sayesinde hesaplanır.
bu hesaplamalarda İntegral sadece bir araçtır. amaç değil. integral kullanım mantığı, kullanıcının belirlenmiş hedeflerine ulaşmak için kullanacağı bir doğrulama aracıdır.
bu sebeple, üniversitelerimizde gösterilen integral tabanlı ders içeriklerinde, öğrencilerin alan bilgisi dahilinde, integralle ilgili hangi yaklaşımları kullanması gerektiği öğretilirse; mühendislik veya diğer alan formasyonları daha iyi kazandırılmış olacaktır.

aklıma gelen bir taş ocağı, koca dağ...
ortalama yoğunluğu belli diyelim sıfır hattına kadar ki, kullanılabilir miktar hesaplanacak, işte integral; burada işinize yarayacak.
artık simson metodu kullanır mısınız, gaus metodu mu yardımcı olur, yoksa başka yardımcı alan bilgileri mi, o size kalmış.
bundan sonra saate bakarken, veya televizyon izlerken, olmadı çatal kullanırken; integrale teşekkür etmeyi unutmayalım.

15 Mayıs 2011 Pazar

KONU ANLATIMLI VİDEOLAR

video3

İNTEGRAL KONU ANLATIMI VİDEOLARI

13 Mayıs 2011 Cuma

İNTEGRALİ ANLATIYORUZ

İNTEGRAL NEDİR?

İntegral, verilen bir f(x) fonksiyonunu türev kabul eden F(x) fonksiyonunun bulunması olarak yapılabilir. F(x) fonksiyonuna f(x) fonksiyonunun integrali veya ilkeli denir. İntegral, Latince toplam kelimesinin ("summa") baş harfi s'nin biraz evrim geçirmiş hali olan ∫ işareti ile gösterilir. Bu işaret Leibniz tarafından tanımlanmıştır.

$F(x) = \int f(x)+ c,$

c bir sabiti gösterir ve integralin bir sabit farkı ile bulunabileceğine işaret eder.

Bir eksen takımında gösterilen f(x) göndermesinin altında kalan a < x < b aralığındaki alan, integral yardımıyla hesaplanabilir. Bu amaçla alan küçük dikdörtgenlere bölünerek, bunların alanı hesap edilip toplanır. Dikdörtgen sayısı arttıkça toplam eğri altındaki alan, alanın değerine yaklaşır ve integralin tam değeri bulunmuş olur. Bu toplama Riemann toplamı denir. İntegralin Riemann anlamındaki tanımıRiemann toplamındaki bölüntü sayısı olan n nin bir limit içerisinde sonsuza götürülmesiyle elde edilir.

$S = \lim_{\Delta x \to 0}\sum_{i=0}^{n-1} f(x_i) \Delta x_{i} = \int_a^b f(x)\,dx = F(b)-F(a)$

Bu şekildeki integral belirli sınırlar arasında hesaplandığı için, belirli İntegral olarak isimlendirilir. Sınırlar göz önüne alınmadan hesaplanan integrale ise belirsiz integral denir. Bazı durumlarda f(x)göndermesinin integrali F(x) bulunamaz. Bu durumda belirli integral sayısal olarak hesaplanır.

Uzunluk, alan ve hacimlerin hesaplanmasında integral hesabın önemli yeri vardır. Birden fazla değişkene bağlı fonksiyonlarda integral kavramı genişletilebilir ve bu durumda katlı integraller ortaya çıkar.

Riemann'dan sonra soyut kümelerin de integrallenebilmesi amacıyla Lebesgue integrali geliştirilmiştir.

İntegralin Formülleri

Rasyonel fonksiyonlar [değiştir]

$\int dx = x + C$

$\int x^n\,{\rm d}x = \frac{x^{n+1}}{n+1} + C\qquad\mbox{ eğer }n \ne -1$

$\int {dx \over x} = \ln{\left|x\right|} + C$

$\int {dx \over {a^2+x^2}} = {1 \over a}\arctan {x \over a} + C$

İrrasyonel fonksiyonlar [değiştir]

$\int {dx \over \sqrt{a^2-x^2}} = \sin^{-1} {x \over a} + C$

$\int {-dx \over \sqrt{a^2-x^2}} = \cos^{-1} {x \over a} + C$

$\int {dx \over x \sqrt{x^2-a^2}} = {1 \over a} \sec^{-1} {|x| \over a} + C$

Logaritmik fonksiyonlar [değiştir]

$\int \ln(x) \,dx = x \ln(x) - x + C,$

$\int \log_b {x}\,dx = x\log_b {x} - x\log_b {e} + C$

Üslü fonksiyonlar [değiştir]

$\int e^x\,dx = e^x + C$

$\int a^x\,dx = \frac{a^x}{\ln{a}} + C$

$\int a^{ln(x)}\,dx =\int x^{ln(a)}\,dx=\frac{x\,a^{ln(x)}}{\ln{a}+1} + C=\frac{x\,x^{ln(a)}}{\ln{a}+1} + C$

Trigonometrik fonksiyonlar [değiştir]

$\int \sin{x}\, dx = -\cos{x} + C$

$\int \cos{x}\, dx = \sin{x} + C$

$\int \tan{x} \, dx = -\ln{\left| \cos {x} \right|} + C$

$\int \cot{x} \, dx = \ln{\left| \sin{x} \right|} + C$

$\int \sec{x} \, dx = \ln{\left| \sec{x} + \tan{x}\right|} + C$

$\int \csc{x} \, dx = \ln{\left| \csc{x} - \cot{x}\right|} + C$

$\int \sec^2 x \, dx = \tan x + C$

$\int \csc^2 x \, dx = -\cot x + C$

$\int \sec{x} \, \tan{x} \, dx = \sec{x} + C$

$\int \csc{x} \, \cot{x} \, dx = - \csc{x} + C$

$\int \sin^2 x \, dx = \frac{1}{2}(x - \sin x \cos x) + C$

$\int \cos^2 x \, dx = \frac{1}{2}(x + \sin x \cos x) + C$

$\int \sec^3 x \, dx = \frac{1}{2}\sec x \tan x + \frac{1}{2}\ln|\sec x + \tan x| + C$

$\int \sin^n x \, dx = - \frac{\sin^{n-1} {x} \cos {x}}{n} + \frac{n-1}{n} \int \sin^{n-2}{x} \, dx$

$\int \cos^n x \, dx = \frac{\cos^{n-1} {x} \sin {x}}{n} + \frac{n-1}{n} \int \cos^{n-2}{x} \, dx$

$\int \arctan{x} \, dx = x \, \arctan{x} - \frac{1}{2} \ln{\left| 1 + x^2\right|} + C$

Hiperbolik fonksiyonlar [değiştir]

$\int \sinh x \, dx = \,cosh x + C$

$\int \cosh x \, dx = \sinh x + C$

$\int \tanh x \, dx = \ln| \cosh x | + C$

$\int \mbox{csch}\,x \, dx = \ln\left| \tanh {x \over2}\right| + C$

$\int \mbox{sech}\,x \, dx = \arctan(\sinh x) + C$

$\int \coth x \, dx = \ln| \sinh x | + C$

$\int \mbox{sech}^2 x\, dx = \tanh x + C$

Ters hiperbolik fonksiyonlar [değiştir]

$\int \operatorname{arcsinh} x \, dx = x \operatorname{arcsinh} x - \sqrt{x^2+1} + C$

$\int \operatorname{arccosh} x \, dx = x \operatorname{arccosh} x - \sqrt{x^2-1} + C$

$\int \operatorname{arctanh} x \, dx = x \operatorname{arctanh} x + \frac{1}{2}\log{(1-x^2)} + C$

$\int \operatorname{arccsch}\,x \, dx = x \operatorname{arccsch} x+ \log{\left[x\left(\sqrt{1+\frac{1}{x^2}} + 1\right)\right]} + C$

$\int \operatorname{arcsech}\,x \, dx = x \operatorname{arcsech} x- \arctan{\left(\frac{x}{x-1}\sqrt{\frac{1-x}{1+x}}\right)} + C$

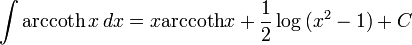
$\int \operatorname{arccoth}\,x \, dx = x \operatorname{arccoth} x+ \frac{1}{2}\log{(x^2-1)} + C$

Belirli İntegral

f : R → R ye tanımlı ve her noktada sürekli ve türevli bir fonksiyon olsun.

f'(x) = F(x) ise

$f(x) = \int F(x)\,dx + C$

olur.

Belirli integral ise alt ve üst sınırlarla belirlendiğinden integral alma işleminden sonra sınırlar ilkel fonksiyona konularak birbirinden çıkarılır ve değer yani fonksiyonun o sınırlar arasında belirttiği alan bulunmuş olur.

Örneğin ; a'dan b'ye kadar F(x) fonksiyonun belirttiği alan (S) ya da alt sınırı : a , üst sınırı : b olan integralin değeri istenirse :

1 - İntegralin önündeki fonksiyonun integrali alınır.

$f(x) = \int F(x)\,dx + C$

olarak bulunur.

2 - Bulunan f(x) fonksiyonuna önce üst sınır (b) verilerek f(b) bulunur.Sonra da alt sınır olan (a) verilir ve f(a) bulunur.

3 - Son aşamada f(b)-f(a) işlemi yapılarak istenen değer ( a ve b arasındaki F(x)'in belirttiği alan (S) ) bulunur.

$S = \int_a^b f(x)\,dx = F(b)-F(a)$

ör.

$\int_4^53x + 2\,dx =( \frac{3}{2}x^2+2x)|_4^5=\frac{31}{2}$

Belirsiz İntegral

Türevi f(x) veya diferansiyeli f(x)dx olan F(x) fonksiyonuna f(x) in belirsiz integrali denir ve

şeklinde gösterilir.

sembolüne integral işareti, f(x) fonksiyonundan F(x) + c fonksiyonunun bulunmasını sağlayan işleme integral alma işlemi,

F(x) + c fonksiyonuna da f(x) in ilkel fonksiyonu denir.

Uyarı

f(x) in integralini bulmak, türevi f(x) e eşit olan fonksiyonu bulmaktır.

Matematik Dünyası