İNTEGRAL NEDİR?
İntegral, verilen bir f(x) fonksiyonunu türev kabul eden F(x) fonksiyonunun bulunması olarak yapılabilir. F(x) fonksiyonuna f(x) fonksiyonunun integrali veya ilkeli denir. İntegral, Latince toplam kelimesinin ("summa") baş harfi s'nin biraz evrim geçirmiş hali olan ∫ işareti ile gösterilir. Bu işaret Leibniz tarafından tanımlanmıştır.
c bir sabiti gösterir ve integralin bir sabit farkı ile bulunabileceğine işaret eder.
Bir eksen takımında gösterilen f(x) göndermesinin altında kalan a < x < b aralığındaki alan, integral yardımıyla hesaplanabilir. Bu amaçla alan küçük dikdörtgenlere bölünerek, bunların alanı hesap edilip toplanır. Dikdörtgen sayısı arttıkça toplam eğri altındaki alan, alanın değerine yaklaşır ve integralin tam değeri bulunmuş olur. Bu toplama Riemann toplamı denir. İntegralin Riemann anlamındaki tanımıRiemann toplamındaki bölüntü sayısı olan n nin bir limit içerisinde sonsuza götürülmesiyle elde edilir.
Bu şekildeki integral belirli sınırlar arasında hesaplandığı için, belirli İntegral olarak isimlendirilir. Sınırlar göz önüne alınmadan hesaplanan integrale ise belirsiz integral denir. Bazı durumlarda f(x)göndermesinin integrali F(x) bulunamaz. Bu durumda belirli integral sayısal olarak hesaplanır.
Uzunluk, alan ve hacimlerin hesaplanmasında integral hesabın önemli yeri vardır. Birden fazla değişkene bağlı fonksiyonlarda integral kavramı genişletilebilir ve bu durumda katlı integraller ortaya çıkar.
Riemann'dan sonra soyut kümelerin de integrallenebilmesi amacıyla Lebesgue integrali geliştirilmiştir.
İntegralin Formülleri
Rasyonel fonksiyonlar [değiştir]
İrrasyonel fonksiyonlar [değiştir]
Logaritmik fonksiyonlar [değiştir]
Üslü fonksiyonlar [değiştir]
Trigonometrik fonksiyonlar [değiştir]
Hiperbolik fonksiyonlar [değiştir]
Ters hiperbolik fonksiyonlar [değiştir]



![\int \operatorname{arccsch}\,x \, dx = x \operatorname{arccsch} x+ \log{\left[x\left(\sqrt{1+\frac{1}{x^2}} + 1\right)\right]} + C](http://upload.wikimedia.org/math/4/c/4/4c4828d0c47957eb215c2249b1c64fa7.png)

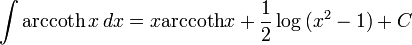
- Belirli İntegral
f'(x) = F(x) ise
olur.
Belirli integral ise alt ve üst sınırlarla belirlendiğinden integral alma işleminden sonra sınırlar ilkel fonksiyona konularak birbirinden çıkarılır ve değer yani fonksiyonun o sınırlar arasında belirttiği alan bulunmuş olur.
Örneğin ; a'dan b'ye kadar F(x) fonksiyonun belirttiği alan (S) ya da alt sınırı : a , üst sınırı : b olan integralin değeri istenirse :
1 - İntegralin önündeki fonksiyonun integrali alınır.
olarak bulunur.
2 - Bulunan f(x) fonksiyonuna önce üst sınır (b) verilerek f(b) bulunur.Sonra da alt sınır olan (a) verilir ve f(a) bulunur.
3 - Son aşamada f(b)-f(a) işlemi yapılarak istenen değer ( a ve b arasındaki F(x)'in belirttiği alan (S) ) bulunur.
ör.

Belirsiz İntegral
Türevi f(x) veya diferansiyeli f(x)dx olan F(x) fonksiyonuna f(x) in belirsiz integrali denir ve
şeklinde gösterilir.
F(x) + c fonksiyonuna da f(x) in ilkel fonksiyonu denir.
Uyarı
f(x) in integralini bulmak, türevi f(x) e eşit olan fonksiyonu bulmaktır. |
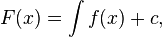



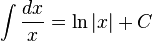

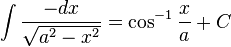



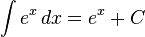
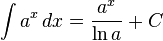




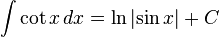








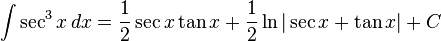
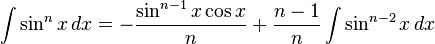











wikipedianın hepsini alsaydınız öyle olmaz
YanıtlaSil